This is a very short research note inspired by a conversation with someone at the ICML 2024 mechanistic interpretability workshop. As such, it’s missing some context that I’d typically supply.

I also just generally have a lot of uncertainty around how to think about this stuff! Please feel free to contact me with corrections.

---

In my recent paper, I trained sparse autoencoders (SAEs) on the first five layers of InceptionV1. One of the interesting findings was a large number of curve detector features—many more than previous work found when studying individual neurons. By design, SAEs represent features as discrete directions, but it’s quite possible that this isn’t how they’re actually represented in the model.

Feature manifolds refer to the concept that certain features, like curve detectors, are not best understood as discrete directions in feature space but rather as points on a continuous manifold. Potentially, it’s more accurate to understand curve features as forming a single manifold that captures variations such as orientation and curvature.

To investigate this, I applied UMAP—a nonlinear dimensionality reduction technique—to the decoder vectors of the curve features. In 2D, this visualization reveals what we might expect if the curve features form a manifold:

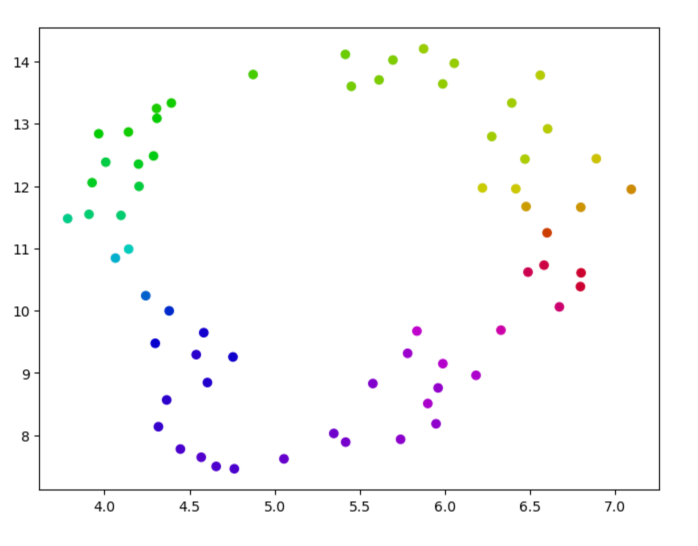
This yields a circle, consistent with the idea of a continuous manifold of curve orientations.

To preserve more of the local structure, I performed a 4D UMAP and then used PCA to project this into 3D and 2D for visualization.

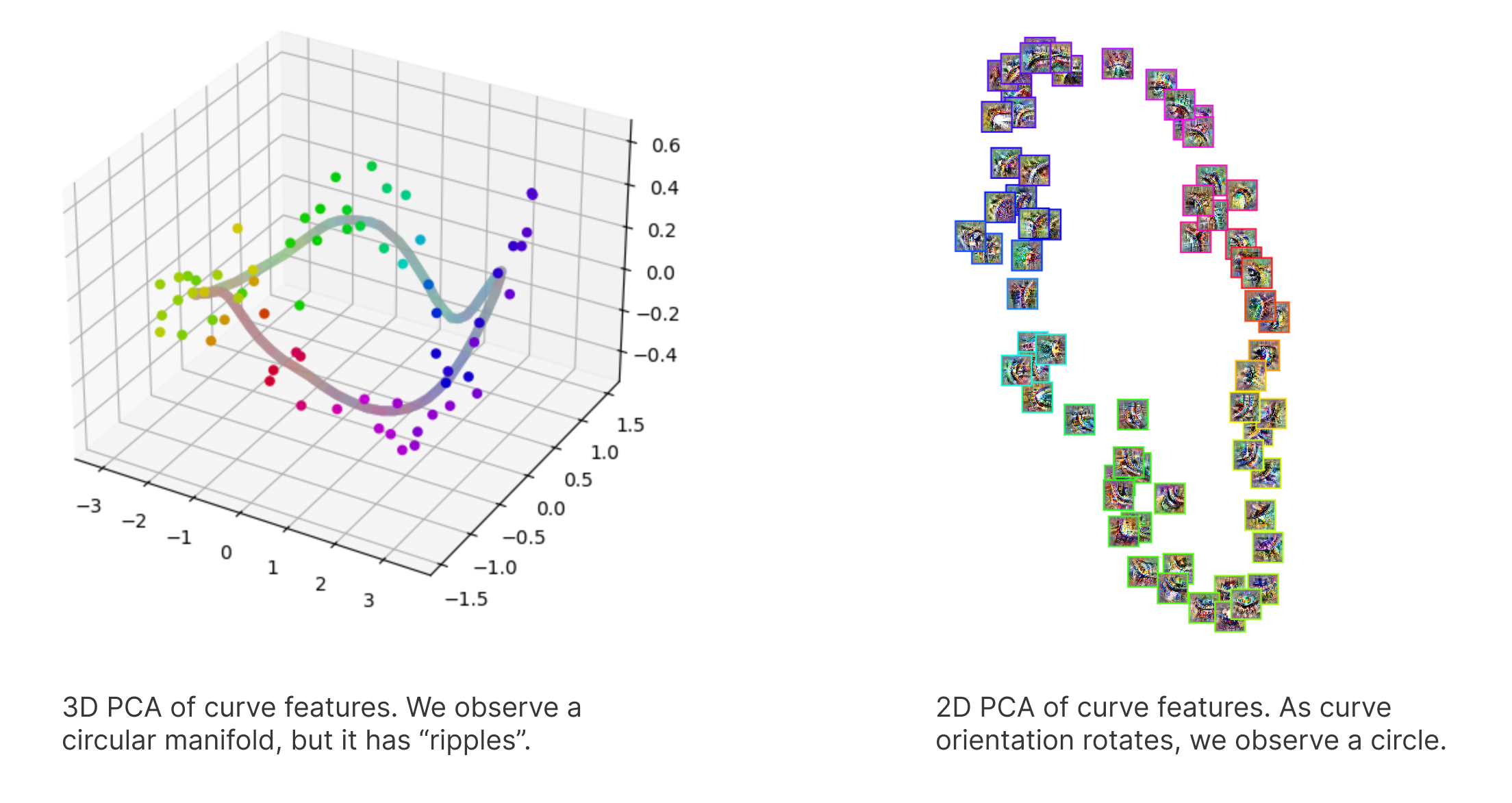
The 2D projection again reveals a circle formed by curve features of different orientations. The 3D PCA reveals something additionally interesting: although still circular, the curve appears to ripple.

The July 2024 update from the Anthropic interpretability team offers a possible explanation for this rippling. They suggest that the model aims to linearly read features without noise, but nearby points on a smooth manifold are almost parallel, making it hard to distinguish between them using linear methods. By rippling the manifold, the model ensures that nearby points have distinct angles, facilitating linear separability and reducing interference between features.

At first, I wasn’t sure what to make of this result, so seeing that update was exciting! The theory makes a lot of sense, and it appears that not only would rippling the manifold be something the model might “want” to do, but it’s something that, at least when it comes to curve detectors, we’re able to observe neatly.

When considering the curve feature manifold, I’m left with a few questions:

What exactly is a curve feature? Is there a “true” set of curve features, or is this notion inherently ill-defined? Does this mean sparse autoencoders, which enforce discrete feature representations, aren’t the right way to capture how models genuinely represent curves? It’s possible that the concept of a discrete curve feature doesn’t fully capture the most fundamental truth about the model. But that doesn’t necessarily diminish their utility as an effective means of understanding InceptionV1.

It also seems quite likely that there isn’t a “true” set of features—that is, a set that both represents the manifold completely and is uniquely the only set to do so. However, perhaps uniqueness isn’t crucial. Recovering the manifold may be sufficient, even if this blurs the definition of features as the fundamental computational units of the model. If our set contains every point on the manifold, then distinguishing between the set and the manifold itself becomes somewhat arbitrary.¹

A well-trained SAE² will learn a set of features that approximates the manifold, but this set isn’t uniquely determined. It seems possible that SAEs are capturing the essence of the curve detectors, albeit in a form that simplifies reasoning and application.

1. To clarify, I’m not suggesting that an ideal set of curve features would consist of discrete directions for every possible point. SAEs with different capacities will recover varying numbers of curve features. Instead, the idea is that by combining these discrete features, we can approximate additional curve orientations. ↩

2. As an aside, I’m uncertain about how we could recover both the manifolds representing continuous features like curves and more discrete features (e.g., a specific dog breed in InceptionV1). While this is an interesting research question, it seems sufficiently challenging that even if SAEs don’t fully capture these aspects, it shouldn’t invalidate their usefulness as tools for advancing our understanding of neural networks—especially regarding safety. ↩