Adversarial examples are poorly understood. There are many different hypotheses that attempt to explain them (which aren’t necessarily exclusive!). One lesser known hypothesis, introduced by Elhage et al, is that the cause might actually be superposition. Elhage et al demonstrate that, in toy models, there’s a very consistent relationship between superposition and vulnerability to adversarial examples:

They also observe that a superposition hypothesis for adversarial examples could explain many observations. However, they’re hesitant to make strong claims based on their limited findings about toy models:

We’re hesitant to speculate about the extent to which superposition is responsible for adversarial examples in practice. There are compelling theories for why adversarial examples occur without reference to superposition (e.g. [35]). But it is interesting to note that if one wanted to try to argue for a “superposition maximalist stance”, it does seem like many interesting phenomena related to adversarial examples can be predicted from superposition. As seen above, superposition can be used to explain why adversarial examples exist. It also predicts that adversarially robust models would have worse performance, since making models robust would require giving up superposition and representing less features. It predicts that more adversarially robust models might be more interpretable (see e.g. [36]). Finally, it could arguably predict that adversarial examples transfer (see e.g. [37]) if the arrangement of features in superposition is heavily influenced by which features are correlated or anti-correlated (see earlier results on this). It might be interesting for future work to see how far the hypothesis that superposition is a significant contributor to adversarial examples can be driven.

I’ve been interested in this hypothesis for a while. Last year, I did a small experiment where I showed that I could “attack” GPT-2 by activating unrelated features which are in superposition with a target feature.

But to the best of my knowledge, no one has done the obvious experiment to test this hypothesis: training sparse autoencoders on adversarially robust models, and comparing to a non-adversarially robust model. Under the superposition hypothesis, one would expect SAEs trained on adversarially robust models to have lower losses. On the other hand, I can’t think of any other hypothesis which would predict such a result.

To test this, I downloaded some of the Madry labs’ old adversarially robust ImageNet models and trained TopK SAEs on ones trained to be robust to different adversarial attacks (both L2 and L-inf), and different attack strengths. I did a very rough hyperparameter sweep for learning rate and then for an expansion factor of 2 trained SAEs for a single epoch on all of ImageNet at varying levels of sparsity (i.e. different values of K). The activation norms of the non-robsut and robust models differ¹ so inputs to the SAE were centered (i.e. zero mean, unit variance using dataset-wide statistics).

I found a consistent trend: for a given level of sparsity, models which are trained to be robust to adversarial attacks have lower SAE losses.

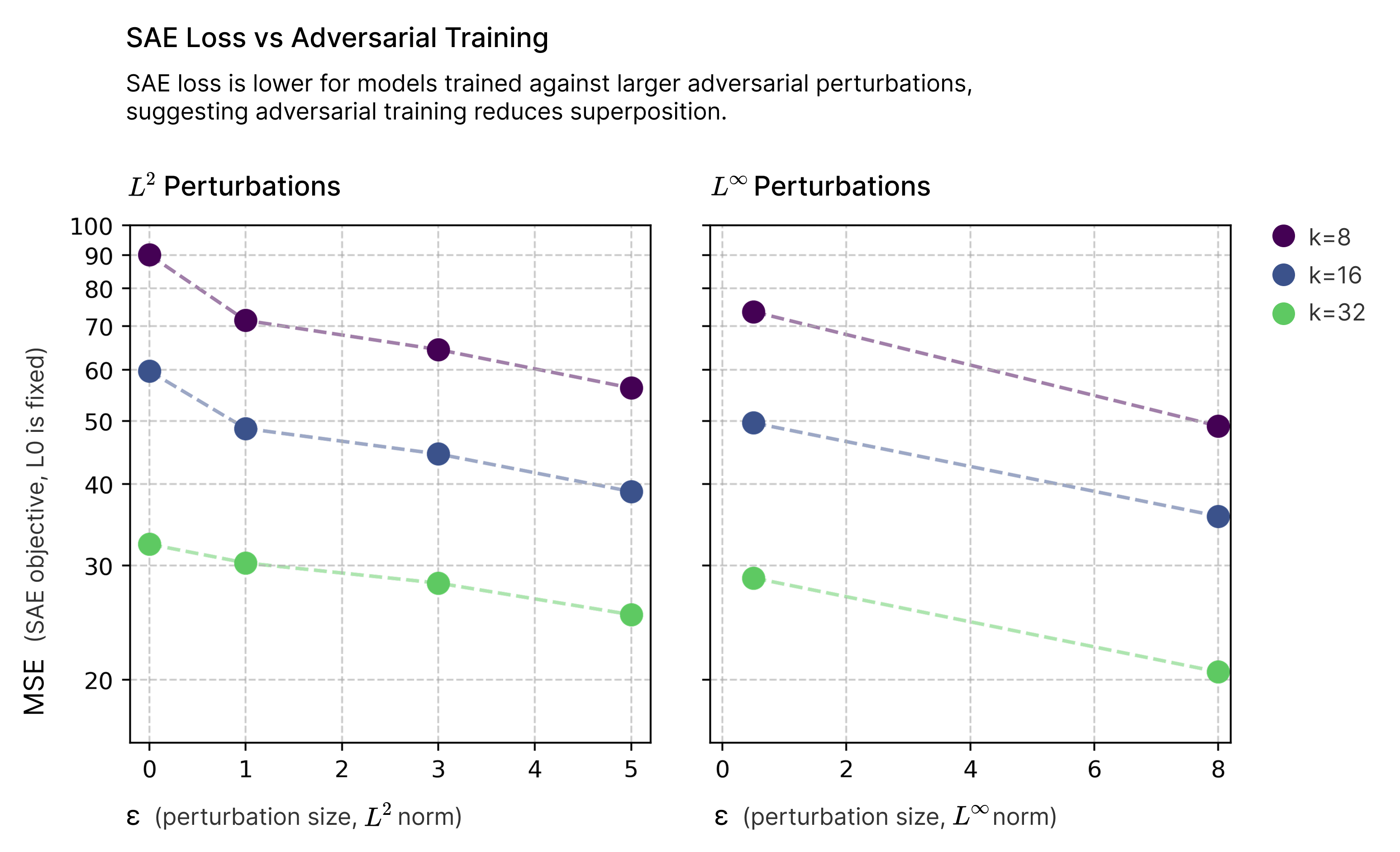
This small experiment adds an interesting data point to our understanding of adversarial examples. While there are many proposed explanations for why neural networks are vulnerable to adversarial attacks, the connection to superposition seems worth investigating further.

If superposition does contribute significantly to adversarial vulnerability, it would suggest some fundamental trade-offs in neural network design between parameter efficiency, model capacity, and robustness.

1. Across all tested models (ImageNet and CIFAR, with both \(L^2\) and \(L^\infty\) robustness), activation distributions showed a consistent pattern: robust models maintained similar min/max ranges as their non-robust counterparts but displayed higher means and standard deviations ↩